系统可靠性预计的方法
胡映
(北方交通大学北京100044)
摘 要:介绍了系统可靠性预计的多种方法。不同的工程阶段对可靠性预计的要求不同,因此预计的目的和用途也不同,相应的就有不同的预计方法。最后介绍了工程中研制复杂系统时在早期设计阶段用于粗略快速预计的方法。
关键词:可靠性预计;电子设备;早期预计;后期预计?
1引言
系统的可靠性预计是以组成系统的各部分的性能、工作环境及相互关系等知识为条件,对系统的固有可靠度进行估算的技术。在工程中应用的具体程序是:在确定元器件、零部件的失效率的基础上,预计由这些元器件、零部件组成的能完成某一功能单元的可靠度,自下而上逐级进行预计,直至最后预计出系统的可靠度。
?系统的可靠性预计,通常分为早期预计和后期预计。
早期预计用于方案论证等初始设计阶段,有元件计数法、上下限法、相似设备法、相似功能法、有源单元法等;
后期预计用于具体设计阶段,有数学模型法、应力分析法、布尔真值法、减额分析法(包括参数变量法、差值分析法、相关法、蒙特卡洛法等用电子计算机进行预计的方法)。
2系统可靠性预计的方法
2.1元件计数法 ?元件计数法是一种按不同种类元器件(电阻器、电容器、二极管、晶体管等)的数量来预计单元和系统可靠度的方法。采用这个方法进行预计,首先确定设计方案中各种元器件的类型。根据GJB29991《电子设备可靠性预计手册》中各类元器件在不考虑工作温度与应力情况下的通用失效率λG以及质量等级πQ和成熟系数πL,计算工作失效率
??λpi=λGπQπL
然后将各类型的元器件数目Ni乘以其失效率λpi,最后对所有的乘积取和,便得系统的失效率λs,即
??λs=ΣNiλpi。
这种方法的优点是,可以快速地进行可靠性预计,以判断某设计方案是否能满足可靠性要求。因此,元器件计数适用于方案论证和早期设计阶段。缺点是准确度较差。
2.2上、下限法 ?上、下限法的基本思想是将复杂的系统先简单的看成是某些单元的串联系统,求出系统可靠度的上限值和下限值。然后逐步考虑系统的复杂情况,逐次求系统可靠度的愈来愈精确的值。
?上、下限法的优点是对复杂系统特别适用。他不要求单元之间是相互独立的,适用于热贮备和冷贮备系统,也适用于多种目的和阶段工作的系统。
在工程应用中具体方法是:首先假定系统中并联部分的可靠度为1,从而忽略了他的影响,这样得到的系统可靠度显然是最高的,这就是上限值;其次假设并联单元不起冗余作用,全部作为串联单元处理,这时处理方法最为简单,但得到的是系统的可靠度最低值,这就是下限值;然后,逐步考虑某些因素以修正上述的上、下限值,最后通过综合公式得到系统的可靠度预计值。
2.3数学模型法 ?所谓数学模型法就是根据组成系统的各单元间的可靠性数学模型,按概率运算法则,预计系统的可靠度的方法,他是一种经典的方法。
?在工程上的具体计算步骤是:建立系统的可靠性逻辑框图及可靠性数学模型,并利用相应的公式,依据已知条件求出系统的可靠度。#p#分页标题#e#
?数学模型法优点是计算比较精确,缺点是比较麻烦,且需要画出系统的逻辑框图。
2.4应力分析法 ?应力分析法的步骤与元件计数法大致相同,只是应力分析法要求更为详细的元器件失效模型和应力数据,故适用于设计后阶段。此方法需涉及到大量的公式和图表。
?用应力分析法预计的步骤是:
(1)计算出单个元器件的工作失效率λp;
(2)将单个元器件的失效率与所用数量相乘,求出该类元器件的失效率;
(3)将各类元器件失效率相加,得出系统的失效率。
2.5布尔真值法 ?这是一种直观计算系统可靠度的方法。其方法是将所有单元列入真值表中,该表有2n行,n列。n是系统中的单元数。表中每一栏填入数值1或0,表示每个单元是完成任务或失效。因此表中列出了所有工作和失效单元的各种可能组合,然后检查真值表的每一行,判断其中工作的和失效的单元的组合是使系统完成任务还是使系统失效。将完成任务的代号S或失效的代号F分别填入真值表的右方一列中,并记下每一个完成任务的成功概率。其成功的概率之和即为系统的可靠度。
2.6蒙特卡洛法 ?蒙特卡洛法是以概率和数理统计为基础,用概率模型做近似计算的一种数学模拟法。他以随机抽样法为手段,根据系统的可靠性方框图进行可靠性预计。当各单元的可靠性特征量已知,但系统的可靠性模型过于复杂,难于推导出一个可以求解的通用公式时,蒙特卡洛法可根据单元完成任务的概率及可靠性方框图,近似计算出系统的可靠度。由于这种方法需反复试验,工作过于繁琐,所以他总是用计算机来完成的。
?蒙特卡洛法规定:每个单元的预计可靠度在可靠性方框图中可以用一组随机数来表示。随机数用计算机的随机数发生器提供。例如,当一个单元的可靠度为0.8时,便可用0~0.799 9中的所有随机数表示单元成功,用0.800 0~0.999 9中的所有随机数表示单元的失效。再根据单元的可靠度及系统的可靠性方框图来预计系统的可靠度。具体的方法如下:
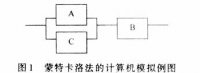
?设某系统的可靠性方框图如图1所示。假设单元A,B,C的可靠度分别为R1、R2、R3。其中第1个单元A(设R1=0.80)用计算机的随机数发生器输入一个随机数,根据第1个随机数来决定这个单元的成功或失效。如果这个随机数小于0.799 9,则表示该单元正常,便应把另1个随机数输入到框图的下一单元B,新的随机数便决定这一单元的成功或失效。

?
如果对单元A发出的随机数大于0.80,但他还有并联单元,则计算机自动返回到最邻近的另一个并联单元C。然后计算机自动给这个并联单元发出一个随机数,与该单元的可靠度比较后,确定其成功或失效。若失效,而系统又没有其他并联单元了,则表示系统失效。上述过程一结束,记下失效次数。若成功,则又对单元?B发出新的随机数,与B单元可靠度比较成功后,则表示系统成功,记下成功次数。这个过程要反复进行到要求的试验次数N?为止。此时,运用大数定律就可计算出系统可靠度的预计值。进行模拟的次数越多,预计值越接近实际情况。图2为蒙特卡洛法的计算机程序流程图。
2.7快速预计法 ?研制新的复杂系统时,在早期设计阶段,对究竟使用哪些元器件及详细数量等并不很清楚,因而不可能也没有必要进行较为精确的计算,这就需要进行粗略的快速预计。
2.7.1图表法
?利用给出的系统的MTBF、n、R关系图表。该图可以在已知系统所含元器件数n和要求该系统MTBF的条件下,求元器件失效率λ。当已知系统所含元器件数n及元器件失效率λ时,可以快速的预计系统能够达到的可靠性水平。图表法虽然简便快速,但误差较大。?
? 
2.7.2相似系统法
?这是一种用从相似系统上获得的特定经验对新设计系统可靠性进行快速预计的方法。系统的可靠性与其内部所在的缺陷是有密切联系的。如果能从原系统上获得系统的失效率与其内部缺陷数目之间的关系常数K,即λ原=Kdi,那么由新系统缺陷总数dr=di+dn-de(di为原有缺陷数,dn为新引进的缺陷数,de为已排除的缺陷数),就可以求出新系统的失效率:
??λ新=Kdr
如果能够估计新系统相对原系统的复杂性,则可预计新系统的失效率为:
??λ新=λ原×相对复杂性系数??
参考文献?
[1]邹桂根.机电一体化系统可靠性设计[M].上海:上海交通大学出版社,1996
[2]居滋培.可靠性工程[M].上海:原子能出版社,2000
[3]田蔚风,金志华.可靠性技术[M].上海:上海交通大学出版社,1996



